Low Thrust 2D Orbital Trajectory Optimization
Ian Ruh
This originated as my final project for the Intro to Optimization course at UW Madison, with Prof. Stephen Wright.
The Jupyter notebook is available here.
Low Thrust 2D Orbital Trajectory Optimization1. Introduction2. Mathematical ModelDiscretizationProblem Model3. SolutionUtility FunctionsFirst Order MethodHermite InterpolationFuel OptimalTime OptimalPseudo Time OptimalPseudo Time Optimal4. Results and DiscussionFuel Optimal ProblemTime Optimal ProblemPseudo Time Optimal Problem5. Conclusion
using PkgPkg.add("JuMP")Pkg.add("PyPlot")Pkg.add("Ipopt")xxxxxxxxxxusing JuMP, PyPlot, Ipopt1. Introduction
Since the first satellites were launched in the late 1950s, engineers and scientists have had to navigate the unfamiliar dynamics of orbital mechanics. The process of getting from point A to point B while in orbit is not an intuitive exercise for someone unfamiliar with how orbital mechanics works because it appears to disobey the laws of physics we are accustomed to in our everyday life.
For example, to launch a rocket, one may think that the objective is to go up so as to get into orbit; after all, the rockets are pointed directly vertical on the launch pads. Yet, the really important factor that determines whether you will stay in space once you have gotten there is how fast you are going sideways. Likewise, if you want to go from one orbit to another orbit, the most natural thing to do is point your rocket in that direction and hit the throttle (and hope any Kerbals get out or your way). That, however, is likely a very inefficient and resource intensive trajectory.
The problem of determining the most efficient way to get from one orbit to another is compounded by the variety of different propulsion systems used on different craft. On the low end (thrust-wise), we have solar sails that use the radiation pressure from the sun (or lasers on earth in some concepts) to alter their velocity. One such example was Mariner 3 (and 4) spacecrafts that used 4 'flaps' on the end of their solar panels to alter the surface area that was presented to the sun, and thus were able to use the radiation pressure for attitude control. Another more recent example is the Planetary Society's crowd-funded Light Sail 2 craft that was launched in 2019. Using a 32 square meter sail, it is able to get an acceleration of 0.058
The most effective (and feasible) trajectories for these vehicles are drastically different. Both in terms of how large a thrust some can provide, and by the fact that most chemical combustion rocket engines have a minimum thrust that if gone below can damage the engine, while other propulsion technologies, including ion thrusters, have fairly low thrusts but can sustain them for very long periods of time.
In this project we look at two of the primary trade offs considered in determining trajectories in the context of a (relatively) low thrust propulsion system: time and fuel.
2. Mathematical Model
For the sake of tractability, the problem has been restricted to considering one body orbiting a much larger body (e.g. a satellite orbiting earth) in a single orbital plane. By limiting ourselves to a single plane, we are able to remove almost half of the orbital parameters that are typically used to define a 3D orbit around a body. Moreover, several additional factors are ignored, including (non-exhaustively) atmospheric effects, gravitational perturbations, and torques due to Earth's bulges.
By making these assumptions, we end up with the dynamics equations below:
Where our state variables are radius (
One significant factor we have to consider here is the gravitational constant
Discretization
We also need to choose a method of discretizing our system. We initially show the results of using the simplest approach to our integration scheme in the first section below, and then proceed with using a much more accurate scheme.
The simplest scheme is forward Euler method where
However, there are many higher order schemes that we can use to increase the accuracy and stability of our model. The scheme we chose here is to use cubic Hermite interpolating polynomials, and integrate those over the domain from 0 to 1. Any cubic polynomial can be uniquely defined by four points, just as a quadratic can be uniquely defined by three, and a line by two. However, we can also uniquely define a cubic polynomial using only two points, and the values of the derivative of the polynomial at those points. The graphs below demonstrate this for several different cases.
xPyPlot.ioff()
"""Utility to evaluate a given cubic hermite polynomial"""function hermitePolynomial(y0, y1, d0, d1) PyPlot.grid("on") f(t) = (2*t^3 - 3*t^2 + 1)*y0 + (t^3 - 2*t^2 + t)*d0 + (-2*t^3 + 3*t^2)*y1 + (t^3 - t^2)*d1 xs = convert(Array, 0:0.01:1) fs = [f(x) for x in xs] PyPlot.plot(xs, fs) axis((0.0,1.0,-0.5,0.5)); xlabel("x") ylabel("y")end
fig = figure("pyplot_subplot_mixed",figsize=(8,8))subplot(221)PyPlot.title("y₀=-0.2, y₁=0.2, d₀=-1, d₁=1")hermitePolynomial(-0.2, 0.2, -1, 1)subplot(222)PyPlot.title("y₀=0, y₁=0, d₀=1, d₁=-1")hermitePolynomial(0, 0, 1, -1)ax = subplot(223)PyPlot.title("y₀=0, y₁=0, d₀=-1, d₁=-1")hermitePolynomial(0, 0, -1, -1)subplot(224)PyPlot.title("y₀=1, y₁=-1, d₀=0, d₁=0")hermitePolynomial(0.5, -0.5, 0, 0)fig.canvas.draw() # Update the figurefig.tight_layout()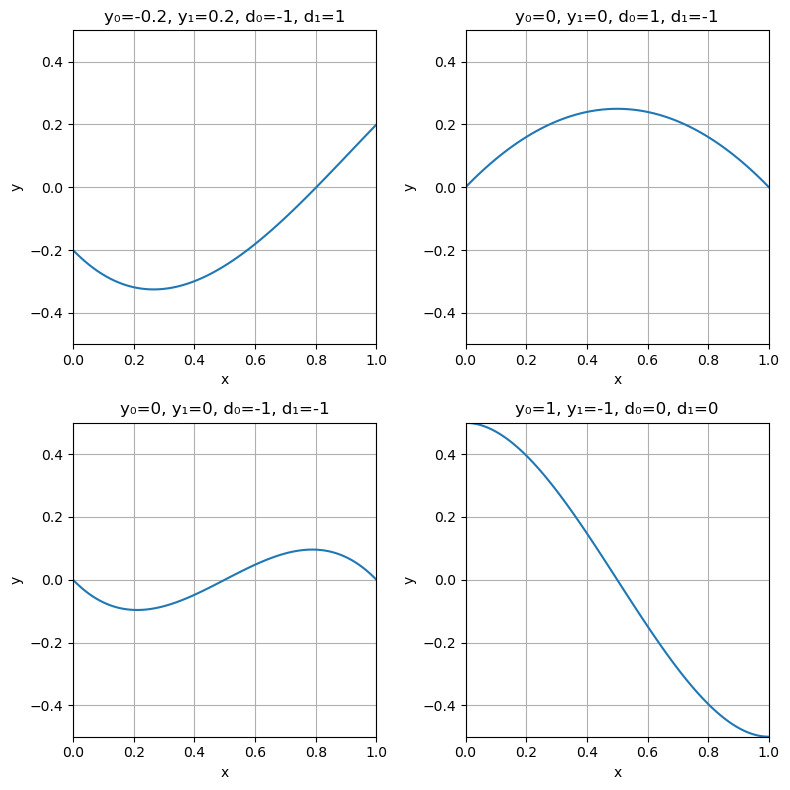
There are two primary reasons these polynomials are useful to us:
- By having control over the derivatives of the polynomials at the end points we are able to make sure that all of our trajectories will be smooth. If the spacecraft in our model is moving at 10 m/s at the end of one segment, it shouldn't be moving at 11 m/s at the beginning of the next, as this would be an unrealistic discontinuity in the model.
- The second reason is that it is very easy to integrate these polynomials. Because they are uniquely defined by the values and derivatives at the two endpoints, the integral over the polynomial from 0 to 1 is also easily expressed in terms of these values:
Using this integration scheme we can achieve a much more accurate and stable system.
Problem Model
Our mathematical model for the fuel optimal problem is:
Where the constraints can be explained as follows:
- All radii should be positive, otherwise we have a degeneracy in our system.
- The thrust can only be positive, and is limited by some maximum thrust the engine can provide.
- The thrust angle can be arbitrarily limited to 0 to
- The initial radius is set.
- The initial tangential velocity is set.
- The initial radial velocity is set.
- The final radius is set.
- The final tangential velocity is set.
- The final radial velocity is set.
In addition, we have a series of N additional sets of constraints for the dynamics of the problem. Below is the first set of constraints for the dynamics, but they only change in the variable indexing for all other steps.
You may have guessed based on the dynamics constraints, but our optimization problem turns out to be non-linear.
3. Solution
Utility Functions
We first define some utility functions below.
xxxxxxxxxx"""A utility function to calculate the tangential velocity required to achieve acircular orbit at a given altitude."""function getCircularVelocity(r) return 1/sqrt(r)endgetCV = getCircularVelocity
"""A function to reconstruct the interpolated values of a cubic Hermite Polynomialbased on the endpoints and derivatives."""function segmentInterp(y0, y1, d0, d1, n_per_segment) f(y0, y1, d0, d1, t) = (2*t^3 - 3*t^2 + 1)*y0 + (t^3 - 2*t^2 + t)*d0 + (-2*t^3 + 3*t^2)*y1 + (t^3 - t^2)*d1 output = [] times = [] for i=1:n_per_segment time = i/n_per_segment push!(output, f(y0, y1, d0, d1, time)) push!(times, time) end return (output, times)end
"""We utilize the linear interpolations for several non-state variables where it would notbe significantly beneficial to use a higher order method."""function linInterp(y0, y1, n_per_segment) f(y0, y1, t) = (y1 - y0)*t + y0 output = [] times = [] for i=1:n_per_segment time = i/n_per_segment push!(output, f(y0, y1, time)) push!(times, time) end return (output, times)end
"""This function just reconstructs and interpolates the statevariables at a higher density than they are solved at.
It has no impact on the results and only serves to have theorbit diagrams more closely reflect what the model issolving."""function reconstructPaths(n_per_segment=50; out_dis) N_original = length(out_dis["r"]) out_interp = Dict() r_new = [] θ_new = [] vr_new = [] vt_new = [] ϕ_new = [] u_new = [] ar_new = [] at_new = [] time_new = [] for i = 1:(N_original-1) (r_seg, time_seg) = segmentInterp(out_dis["r"][i], out_dis["r"][i+1], out_dis["vr"][i], out_dis["vr"][i+1], n_per_segment) (θ_seg, time_seg) = linInterp(out_dis["θ"][i], out_dis["θ"][i+1], n_per_segment) (vr_seg, time_seg) = linInterp(out_dis["vr"][i], out_dis["vr"][i+1], n_per_segment) (vt_seg, time_seg) = linInterp(out_dis["vt"][i], out_dis["vt"][i+1], n_per_segment) (ϕ_seg, time_seg) = linInterp(out_dis["ϕ"][i], out_dis["ϕ"][i+1], n_per_segment) (u_seg, time_seg) = linInterp(out_dis["u"][i], out_dis["u"][i+1], n_per_segment) (ar_seg, time_seg) = linInterp(out_dis["ar"][i], out_dis["ar"][i+1], n_per_segment) (at_seg, time_seg) = linInterp(out_dis["at"][i], out_dis["at"][i+1], n_per_segment) r_new = vcat(r_new, r_seg) θ_new = vcat(θ_new, θ_seg) vr_new = vcat(vr_new, vr_seg) vt_new = vcat(vt_new, vt_seg) ϕ_new = vcat(ϕ_new, ϕ_seg) u_new = vcat(u_new, u_seg) ar_new = vcat(ar_new, ar_seg) at_new = vcat(at_new, at_seg) time_new = vcat(time_new, time_seg .+ out_dis["t"][i]) end return Dict( "r" => r_new, "θ" => θ_new, "vr" => vr_new, "vt" => vt_new, "ϕ" => ϕ_new, "u" => u_new, "ar" => ar_new, "at" => at_new, "t" => time_new ) end
"""Given a solved trajectory, determine how long it takes to get to a given orbit."""function timeToOrbit(outputs, r_final) r_delta = 0.01 vt_delta = 0.01 vr_delta = 0.01 for i in 1:(size(outputs["t"])[1]-1) if(outputs["r"][i] < r_final + r_delta && outputs["r"][i] > r_final - r_delta && outputs["vr"][i] < vr_delta && outputs["vr"][i] > -1*vr_delta && outputs["vt"][i] < getCV(r_final) + vt_delta && outputs["vt"][i] > getCV(r_final) - vt_delta) return outputs["t"][i] end endend
"""Given a solved trajectory, determine how much fuel is used."""function fuelUsed(outputs) total = 0.0 for i in 1:(size(outputs["t"])[1]-2) total += outputs["u"][i]*(outputs["t"][i+1] - outputs["t"][i]) end return totalend
"""Given a solved trajectory, how many thrust segments were there."""function thrustSegments(outputs) total = 0 thrusting = false for i in 1:(size(outputs["t"])[1]) if(outputs["u"][i] > 0.0005 && thrusting == false) thrusting = true total += 1 elseif(outputs["u"][i] <= 0.0005 && thrusting == true) thrusting = false end end return totalendFirst Order Method
In this example we demonstrate the limitations of using a first order accurate integration scheme. Refer to the comments for a description of what each line/section does.
xxxxxxxxxx"""This function builds and runs our model to optimize the orbital trajectory.
Parameters:- r_init: The initial radius- r_final: The final radius- N: The number of segments to use- T: The total time period to simulate for"""function transferOrbit(;r_init, r_final, N, T) # Model options μ = 1 # Gravitational constant max_thrust = 0.1 # Maximum thrust # Calculated values dt = T/N
# Declare model model = Model()
# Declare our models variables (model, r[1:N] >= 0) # Radius state variable (model, θ[1:N]) # Phase state variable (model, vr[1:N]) # Radial velocity state variable (model, vt[1:N]) # Tangential velocity state variable (model, ϕ[1:N]) # Thrust angle control variable (model, u[1:N] >= 0) # Thrust magnitude control variable # Initial Conditions (circular at an altitude of r_init) (model, r[1] == r_init) (model, θ[1] == 0) (model, vr[1] == 0) (model, vt[1] == getCV(r_init)) # Misc Constraints (model, u .<= max_thrust) # Limit the amount of thrust that can be provided (model, ϕ .<= 2*pi) (model, ϕ .>= 0)
# Final state constraint (circular orbit at an altitude of r_final) (model, r[N] == r_final) (model, vr[N] == 0) (model, vt[N] == getCV(r_final)) # Dynamics constraints for i in 2:N # Using just forward euler to integrate the state variables according to the dynamics equations (model, r[i] - r[i-1] == dt*(vr[i-1] + vr[i]) /2) (model, θ[i] - θ[i-1] == dt*(vt[i-1]/r[i-1] + vt[i]/r[i]) /2) (model, vr[i] - vr[i-1] == dt*(vt[i-1]^2/r[i-1] - μ/r[i-1]^2 + u[i-1]*sin(ϕ[i-1]) + vt[i]^2/r[i] - μ/r[i]^2 + u[i]*sin(ϕ[i])) /2) (model, vt[i] - vt[i-1] == dt*(u[i-1]*cos(ϕ[i-1]) - vr[i-1]*vt[i-1]/r[i-1] + u[i]*cos(ϕ[i]) - vr[i]*vt[i]/r[i]) /2)
end # Our objective is to change our orbit using the minimum amount # of fuel possible. (model, Min, sum(u)) # We set the optimizer to use for the problem set_optimizer(model, with_optimizer(Ipopt.Optimizer)); set_optimizer_attribute(model, "print_level", 3); optimize!(model) # Collect and return the model's variables r_final = value.(r) θ_final = value.(θ) vr_final = value.(vr) vt_final = value.(vt) ϕ_final = value.(ϕ) u_final = value.(u) return (r_final, θ_final, vr_final, vt_final, ϕ_final, u_final)endNow, after defining our model, we can run it. We look at a trajectory starting at a radius of two and raising it to three.
xxxxxxxxxx(r_final, theta_final, vr_final, vt_final, phi_final, u_final) = transferOrbit( r_init = 2.0, # Initial orbit radius r_final = 3.0, # Final orbit radius N = 100, # Number of segments T = 12.0, # Total time period)xxxxxxxxxx******************************************************************************This program contains Ipopt, a library for large-scale nonlinear optimization.Ipopt is released as open source code under the Eclipse Public License (EPL).For more information visit http://projects.coin-or.org/Ipopt******************************************************************************Total number of variables............................: 600variables with only lower bounds: 200variables with lower and upper bounds: 0variables with only upper bounds: 0Total number of equality constraints.................: 403Total number of inequality constraints...............: 300inequality constraints with only lower bounds: 100inequality constraints with lower and upper bounds: 0inequality constraints with only upper bounds: 200
xxxxxxxxxxNumber of Iterations....: 275(scaled) (unscaled)Objective...............: 1.2906157047443689e+00 1.2906157047443689e+00Dual infeasibility......: 5.8214176803101869e-09 5.8214176803101869e-09Constraint violation....: 2.7176964021227712e-14 2.7176964021227712e-14Complementarity.........: 9.0912510740244202e-10 9.0912510740244202e-10Overall NLP error.......: 5.8214176803101869e-09 5.8214176803101869e-09
xxxxxxxxxxNumber of objective function evaluations = 437Number of objective gradient evaluations = 270Number of equality constraint evaluations = 437Number of inequality constraint evaluations = 437Number of equality constraint Jacobian evaluations = 296Number of inequality constraint Jacobian evaluations = 296Number of Lagrangian Hessian evaluations = 275Total CPU secs in IPOPT (w/o function evaluations) = 3.830Total CPU secs in NLP function evaluations = 1.325EXIT: Optimal Solution Found.
xxxxxxxxxxfig = figure(figsize=(10,10)) # Create a new figureax = PyPlot.axes(polar="true") # Create a polar axisPyPlot.title("Fuel Optimum Transfer Trajectory")p = plot(theta_final,r_final,linestyle="-",marker="None") # Basic line plot
dtheta = 10ax.set_thetagrids(collect(0:dtheta:360-dtheta)) # Show grid lines from 0 to 360 in increments of dthetaax.set_theta_zero_location("N") # Set 0 degrees to the top of the plotax.set_theta_direction(-1) # Switch to clockwisefig.canvas.draw() # Update the figure
fig = figure("pyplot_subplot_mixed",figsize=(10,4))subplot(221)plot(u_final);title("Thrust")subplot(222)plot(phi_final);title("Thrust Angle")subplot(223)plot(vt_final);title("Tangential Velocity")subplot(224)plot(vr_final);title("Radial Velocity")fig.canvas.draw() # Update the figurefig.tight_layout()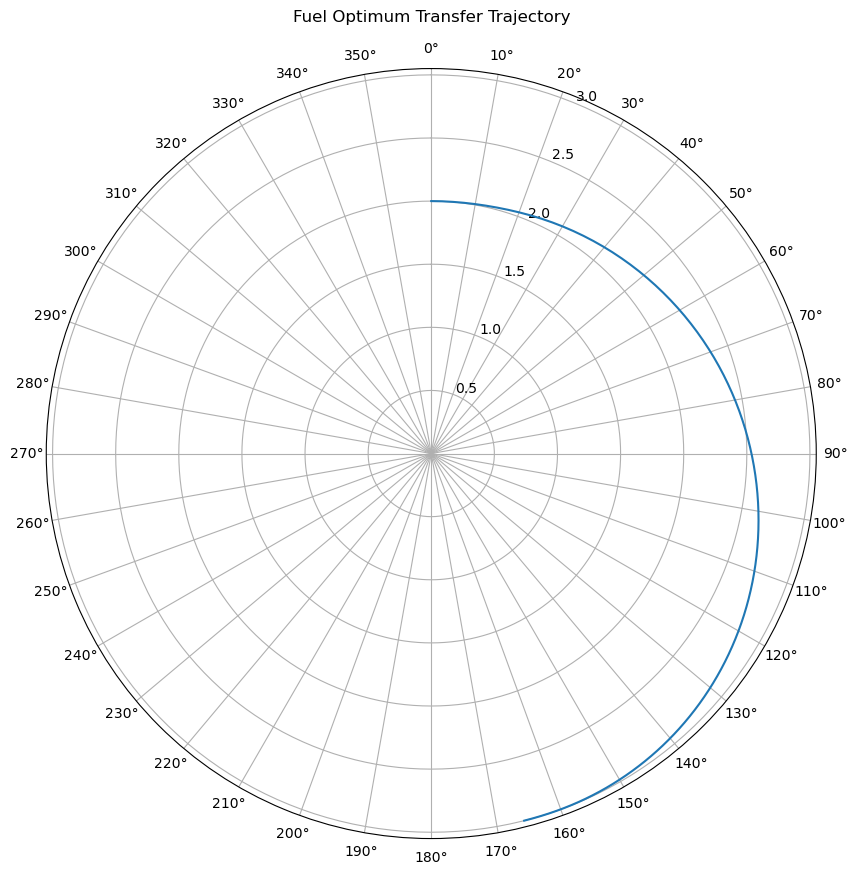
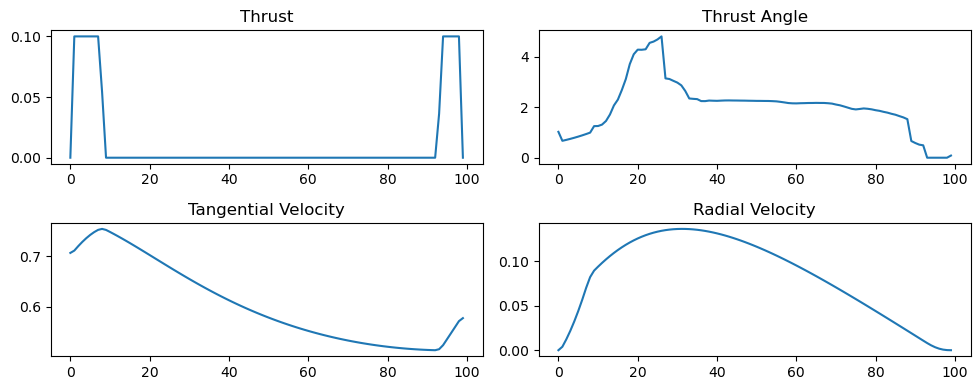
Saving some more in depth discussions of the results here for when we get more accurate trajectories in the next section, we'll just note a couple of items.
- The thrust angle graph looks weird. It is weird, because it is largely meaningless. The thrust angle is unconstrained by the model when the thrust is equal to zero, as it doesn't matter what direction your engine is pointing if it isn't turned on. Only the angles when the thrust is non-zero are physically relevant.
- Second, we can qualitatively compare this observed orbit to a Hohmann transfer, and immediately see the similarities. We start from a circular orbit, get into an elliptical orbit with an apoapsis at the level of our target orbit, then raise the periapsis when we get to the apoapsis.
Next, we'll demonstrate the instability in our current model by just increasing our simulation time a little bit. In the previous run, we used
xxxxxxxxxx(r_final, theta_final, vr_final, vt_final, phi_final, u_final) = transferOrbit( r_init = 2.0, # Initial orbit radius r_final = 3.0, # Final orbit radius N = 100, # Number of segments T = 16.0, # Total time period)xxxxxxxxxxTotal number of variables............................: 600variables with only lower bounds: 200variables with lower and upper bounds: 0variables with only upper bounds: 0Total number of equality constraints.................: 403Total number of inequality constraints...............: 300inequality constraints with only lower bounds: 100inequality constraints with lower and upper bounds: 0inequality constraints with only upper bounds: 200Number of Iterations....: 3000(scaled) (unscaled)Objective...............: 5.3773910687749185e+00 5.3773910687749185e+00Dual infeasibility......: 1.0478741122425304e+00 1.0478741122425304e+00Constraint violation....: 2.0851140079821096e+00 3.1121554823118458e+03Complementarity.........: 3.4364842033426444e-03 3.4364842033426444e-03Overall NLP error.......: 2.0851140079821096e+00 3.1121554823118458e+03Number of objective function evaluations = 33821Number of objective gradient evaluations = 354Number of equality constraint evaluations = 33821Number of inequality constraint evaluations = 33821Number of equality constraint Jacobian evaluations = 3048Number of inequality constraint Jacobian evaluations = 3048Number of Lagrangian Hessian evaluations = 3000Total CPU secs in IPOPT (w/o function evaluations) = 22.633Total CPU secs in NLP function evaluations = 7.238EXIT: Maximum Number of Iterations Exceeded.
If you look at the output above closely, you'll see that the solver didn't actually converge to a solution. We can still look at its outputs though and see where it ended up:
xxxxxxxxxxfig = figure(figsize=(10,10)) # Create a new figureax = PyPlot.axes(polar="true") # Create a polar axisPyPlot.title("Unstable Transfer Trajectory")p = plot(theta_final,r_final,linestyle="-",marker="None") # Basic line plot
dtheta = 10ax.set_thetagrids(collect(0:dtheta:360-dtheta)) # Show grid lines from 0 to 360 in increments of dthetaax.set_theta_zero_location("N") # Set 0 degrees to the top of the plotax.set_theta_direction(-1) # Switch to clockwisefig.canvas.draw() # Update the figure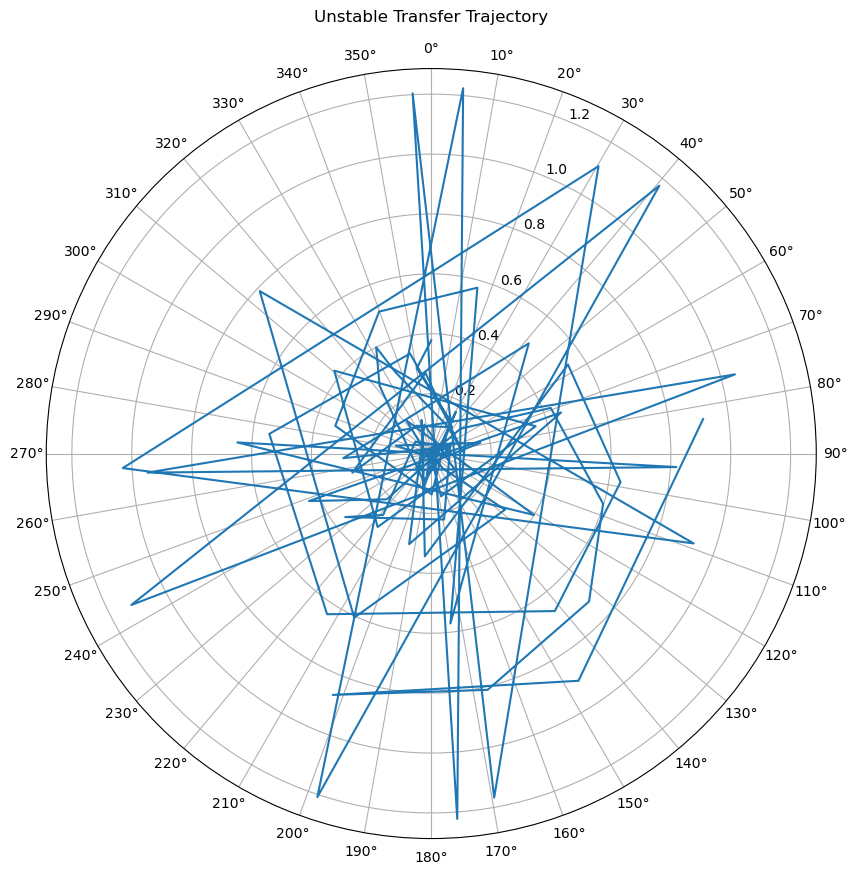
Clearly this doesn't seem likely to be a good prediction of reality. It probably also violates several laws of physics if we cared to do the math.
This is just to show the importance of the numerical scheme used in the model. In the next section we construct a very similar model, but use the higher order integration scheme described before, namely integrating cubic Hermite interpolating polynomials. Note the time steps we used above (on the order of
Hermite Interpolation
Below we construct the model using the integration scheme described in the introduction, and using a fuel optimal or a pseudo-time optimal objective function, which is discussed in the results section.
xxxxxxxxxx Objectives fuelOptimal pseudoTime
"""Parameters:- λ1 is the penalty parameter for the pseudo time optimal objective- modelObjective chooses which objective function to use- T is the total time horizon- N is the number of nodes- max_thrust is the maximum thrust that can be applied- r_init is the initial orbit radius- r_final is the final orbit radius"""function transferOrbitHermite(λ1; modelObjective, T, N, max_thrust, r_init, r_final) # Model options μ = 1 # Gravitational constant # Calculated values dt = T/N
# Declare model model = Model()
# Declare our models variables (model, r[1:N] >= 0) (model, θ[1:N]) (model, vr[1:N]) (model, vt[1:N]) (model, ar[1:N]) (model, at[1:N]) (model, ϕ[1:N]) (model, u[1:N] >= 0) # Slack variable for pseudo time optimal (model, slackR[1:N]) # Starting Values (starts everything in circular orbit at the initial altitude) set_start_value.(u, zeros(N)) set_start_value.(ϕ, zeros(N)) set_start_value.(r, r_init*ones(N)) set_start_value.(vr, zeros(N)) set_start_value.(vt, getCV(r_init)*ones(N)) set_start_value.(ar, zeros(N)) set_start_value.(at, zeros(N)) # Initial Conditions (circular orbit at given radius) (model, r[1] == r_init) (model, θ[1] == 0) (model, vr[1] == 0) (model, vt[1] == getCV(r_init)) # Misc Constraints (model, u .<= max_thrust) (model, ϕ .<= 2*pi - 1e-9) # Approximate strict inequality (doesn't really work) (model, ϕ .>= 0)
# Final state constraint (circular orbit at given radius) (model, r[N] == r_final) (model, vr[N] == 0) (model, vt[N] == getCV(r_final)) # Dynamics constraints (model, at[1] == (vt[2] - vt[1])/dt) (model, ar[1] == (vr[2] - vr[1])/dt) for i in 2:N # Indexing variables istart = i-1; iend = i; # Radial (model, r[iend] - r[istart] == dt*(vr[istart]/2 + vr[iend]/2 + ar[istart]/12 - ar[iend]/12)) # Phase (model, θ[iend] - θ[istart] == dt*(vt[istart]/r[istart]/2 + vt[iend]/r[iend]/2 + 1/12*(at[istart]/r[istart] - vt[istart]*vr[istart]/r[istart]^2) - 1/12*(at[iend]/r[iend] - vt[iend]*vr[iend]/r[iend]^2))) # Radial acceleration if(i < N) (model, ar[i] == (vr[i+1] - vr[i-1])/2/dt) elseif(i == N) (model, ar[i] == (vr[i] - vr[i-1])/dt) end # Radial Velocity (model, vr[iend] - vr[istart] == dt*( (1/2)*(vt[istart]^2/r[istart] - μ/r[istart]^2+u[istart]*sin(ϕ[istart])) + (1/2)*(vt[iend]^2/r[iend] - μ/r[iend]^2+u[iend]*sin(ϕ[iend])) + (1/12)*(2*vt[istart]*at[istart]/r[istart] - vt[istart]^2*vr[istart]/r[istart]^2 + 2*μ/r[istart]^3*vr[istart] + (u[iend]-u[istart])/dt*sin(ϕ[istart]) + u[istart]*(ϕ[iend]-ϕ[istart])/dt*cos(ϕ[istart])) - (1/12)*(2*vt[iend]*at[iend]/r[iend] - vt[iend]^2*vr[iend]/r[iend]^2 + 2*μ/r[iend]^3*vr[iend] + (u[iend]-u[istart])/dt*sin(ϕ[iend]) + u[iend]*(ϕ[iend]-ϕ[istart])/dt*cos(ϕ[iend])) )) # Tangential acceleration if(i < N) (model, at[i] == (vt[i+1] - vt[i-1])/2/dt) elseif(i == N) (model, at[i] == (vt[i] - vt[i-1])/dt) end # Tangential Velocity (model, vt[iend] - vt[istart] == dt*( (1/2)*(-1*vr[istart]*vt[istart]/r[istart] + u[istart]*cos(ϕ[istart])) + (1/2)*(-1*vr[iend]*vt[iend]/r[iend] + u[iend]*cos(ϕ[iend])) + (1/12)*(vr[istart]^2*vt[istart]/r[istart]^2 - (vr[istart]*at[istart]+ar[istart]*vt[istart])/r[istart] - u[istart]*sin(ϕ[istart])*(ϕ[iend]-ϕ[istart])/dt + (u[iend]-u[istart])/dt*cos(ϕ[istart])) - (1/12)*(vr[iend]^2*vt[iend]/r[iend]^2 - (vr[iend]*at[iend]+ar[iend]*vt[iend])/r[iend] - u[iend]*sin(ϕ[iend])*(ϕ[iend]-ϕ[istart])/dt + (u[iend]-u[istart])/dt*cos(ϕ[iend])) ))
end # Slack constraints (model, slackR .>= r .- r_final) (model, slackR .>= -1(r .- r_final)) # Choose the objective function if(modelObjective == fuelOptimal) (model, Min, sum(u)) elseif(modelObjective == pseudoTime) (model, Min, sum(u) + λ1*sum(slackR)) else # Default to fuel optimal (model, Min, sum(u)) end # Solve the problem set_optimizer(model, with_optimizer(Ipopt.Optimizer)); set_optimizer_attribute(model, "print_level", 3); optimize!(model) # Output the results r_out = value.(r) θ_out = value.(θ) vr_out = value.(vr) vt_out = value.(vt) ar_out = value.(ar) at_out = value.(at) ϕ_out = value.(ϕ) u_out = value.(u) return Dict( "r" => r_out, "θ" => θ_out, "vr" => vr_out, "vt" => vt_out, "ϕ" => ϕ_out, "u" => u_out, "ar" => ar_out, "at" => at_out, "t" => convert(Array, 0:dt:T) )endxxxxxxxxxx"""This is simply a utility function to run a simulation and plot its outputs."""function runHermite(plotTitle, λ1=0.0;modelObjective, T, N, max_thrust, r_init, r_final) output = transferOrbitHermite( λ1, modelObjective=modelObjective, T=T, N=N, max_thrust=max_thrust, r_init=r_init, r_final=r_final ) output = reconstructPaths(out_dis=output) fig = figure(figsize=(10,10)) # Create a new figure ax = PyPlot.axes(polar="true") # Create a polar axis PyPlot.title(plotTitle) p = scatter(output["θ"][end:-1:1], output["r"][end:-1:1], c=output["u"][end:-1:1], cmap="jet", s=1.0)
dtheta = 10 ax.set_thetagrids(collect(0:dtheta:360-dtheta)) # Show grid lines from 0 to 360 in increments of dtheta ax.set_theta_zero_location("N") # Set 0 degrees to the top of the plot ax.set_theta_direction(-1) # Switch to clockwise ax[:set_yticks](convert(Array, 0:0.5:r_final+0.5)) color_bar = PyPlot.colorbar() color_bar.set_label("Thrust") fig.canvas.draw() # Update the figure fig = figure("pyplot_subplot_mixed",figsize=(10,6)) subplot(321) plot(output["t"], output["r"]); title("Radius") subplot(322) plot(output["t"], output["u"]); title("Thrust") subplot(323) plot(output["t"], output["ϕ"] .% (2*pi)); title("Thrust Angle") subplot(324) plot(output["t"], output["vt"]); title("Tangential Velocity") subplot(325) plot(output["t"], output["vr"]); title("Radial Velocity") subplot(326) plot(output["t"], output["θ"]); title("Phase") fig.canvas.draw() # Update the figure suptitle("Transfer Orbit Profiles") fig.tight_layout()endFuel Optimal
We do a fuel optimal transfer orbit from a height of 2 to a height of 6. Notice, we also use a time step of 1.5, 15 times larger than for the simple integration scheme, and this isn't even very close to the limit of the model's stability.
xxxxxxxxxxrunHermite( "Fuel Optimum Transfer Trajectory", modelObjective=fuelOptimal, T=300.0, N=200, max_thrust=0.002, r_init=2.0, r_final=6.0)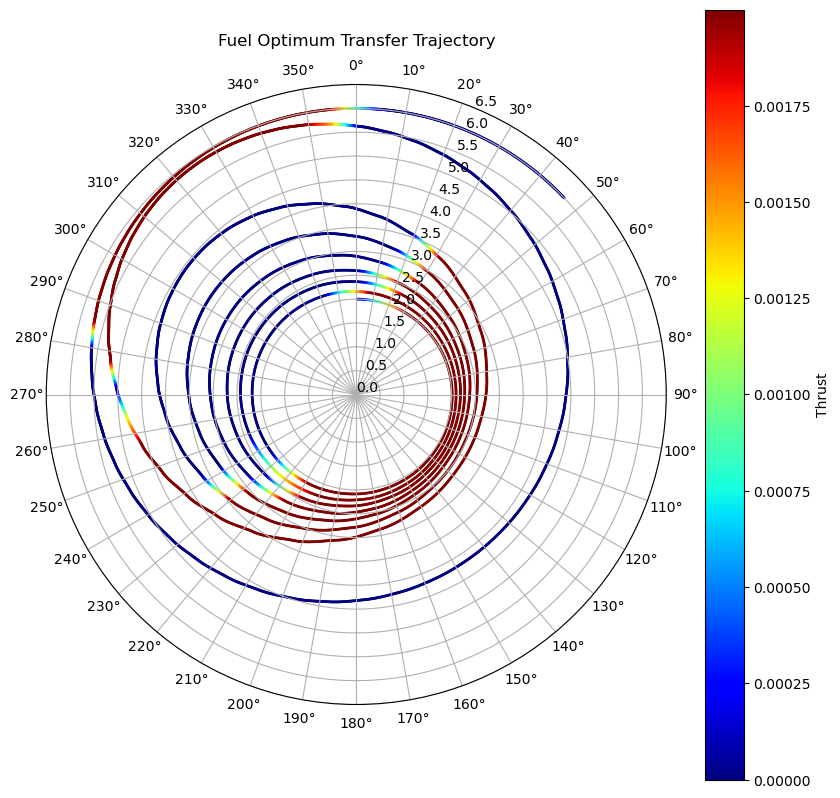

xxxxxxxxxxTotal number of variables............................: 1800variables with only lower bounds: 400variables with lower and upper bounds: 0variables with only upper bounds: 0Total number of equality constraints.................: 1203Total number of inequality constraints...............: 1000inequality constraints with only lower bounds: 600inequality constraints with lower and upper bounds: 0inequality constraints with only upper bounds: 400Number of Iterations....: 165(scaled) (unscaled)Objective...............: 1.9469062148290456e-01 1.9469062148290456e-01Dual infeasibility......: 1.7590151557556055e-11 1.7590151557556055e-11Constraint violation....: 5.9952043329758453e-15 5.9952043329758453e-15Complementarity.........: 2.5059035601177880e-09 2.5059035601177880e-09Overall NLP error.......: 2.5059035601177880e-09 2.5059035601177880e-09Number of objective function evaluations = 263Number of objective gradient evaluations = 166Number of equality constraint evaluations = 263Number of inequality constraint evaluations = 263Number of equality constraint Jacobian evaluations = 166Number of inequality constraint Jacobian evaluations = 166Number of Lagrangian Hessian evaluations = 165Total CPU secs in IPOPT (w/o function evaluations) = 2.490Total CPU secs in NLP function evaluations = 1.755EXIT: Optimal Solution Found.
We can assess the optimality of this trajectory based on the qualitative shape of the thrust profile. Due to the nature of the system's dynamics, it is most efficient to raise the apoapsis while at the periapsis, and it is most efficient to raise the periapsis while at the highest apoapsis. These two factors contribute to making the optimal thrust profile a 'bang bang' profile, where there is a thrust arc around every periapsis, and then a few thrust arcs near the highest apoapsis to circularize the orbit.
By the nature of how we structured the problem, this is a fuel optimal transfer trajectory subject to a maximum time of 300.0. In the next section we explore how we can get time optimal trajectories, with varying degrees of success.
Time Optimal
The problem modeled below is very similar to the problem laid out in the fuel optimal case. However, we now just make the time step size one of the variables we optimize over, and try to minimize
xxxxxxxxxx"""Parameters:T is the total time horizonN is the number of nodesmax_thrust is the maximum thrust that can be applied"""function transferOrbitHermiteTime(λ1, λ2, λ3 ;N, max_thrust, r_init, r_final) # Model options μ = 1 # Gravitational constant
# Declare model model = Model()
# Declare our models variables (model, r[1:N] >= 0) (model, θ[1:N]) (model, vr[1:N]) (model, vt[1:N]) (model, ar[1:N]) (model, at[1:N]) (model, dt >= 0) (model, ϕ[1:N]) (model, u[1:N] >= 0) # Starting Values (starts everything in circular orbit at the initial altitude) set_start_value.(u, zeros(N)) set_start_value.(ϕ, zeros(N)) set_start_value.(r, r_init*ones(N)) set_start_value.(vr, zeros(N)) set_start_value.(vt, getCV(r_init)*ones(N)) set_start_value.(ar, zeros(N)) set_start_value.(at, zeros(N)) set_start_value(dt, 200.0/N) # Initial Conditions (model, r[1] == r_init) (model, θ[1] == 0) (model, vr[1] == 0) (model, vt[1] == getCV(r_init)) # Misc Constraints (model, u .<= max_thrust) (model, ϕ .<= 2*pi - 1e-9) # Approximate strict inequality (model, ϕ .>= 0) (model, dt <= 400.0/N)
# Final state constraint (model, r[N] == r_final) (model, vr[N] == 0) (model, vt[N] == getCV(r_final)) # Dynamics constraints (model, at[1] == (vt[2] - vt[1])/dt) (model, ar[1] == (vr[2] - vr[1])/dt) for i in 2:N istart = i-1; iend = i; # Radial (model, r[iend] - r[istart] == dt*(vr[istart]/2 + vr[iend]/2 + ar[istart]/12 - ar[iend]/12)) # Phase (model, θ[iend] - θ[istart] == dt*(vt[istart]/r[istart]/2 + vt[iend]/r[iend]/2 + 1/12*(at[istart]/r[istart] - vt[istart]*vr[istart]/r[istart]^2) - 1/12*(at[iend]/r[iend] - vt[iend]*vr[iend]/r[iend]^2))) # Radial acceleration if(i < N) (model, ar[i] == (vr[i+1] - vr[i-1])/2/dt) elseif(i == N) (model, ar[i] == (vr[i] - vr[i-1])/dt) end # Radial Velocity (model, vr[iend] - vr[istart] == dt*( (1/2)*(vt[istart]^2/r[istart] - μ/r[istart]^2+u[istart]*sin(ϕ[istart])) + (1/2)*(vt[iend]^2/r[iend] - μ/r[iend]^2+u[iend]*sin(ϕ[iend])) + (1/12)*(2*vt[istart]*at[istart]/r[istart] - vt[istart]^2*vr[istart]/r[istart]^2 + 2*μ/r[istart]^3*vr[istart] + (u[iend]-u[istart])/dt*sin(ϕ[istart]) + u[istart]*(ϕ[iend]-ϕ[istart])/dt*cos(ϕ[istart])) - (1/12)*(2*vt[iend]*at[iend]/r[iend] - vt[iend]^2*vr[iend]/r[iend]^2 + 2*μ/r[iend]^3*vr[iend] + (u[iend]-u[istart])/dt*sin(ϕ[iend]) + u[iend]*(ϕ[iend]-ϕ[istart])/dt*cos(ϕ[iend])) )) # Tangential acceleration if(i < N) (model, at[i] == (vt[i+1] - vt[i-1])/2/dt) elseif(i == N) (model, at[i] == (vt[i] - vt[i-1])/dt) end # Tangential Velocity (model, vt[iend] - vt[istart] == dt*( (1/2)*(-1*vr[istart]*vt[istart]/r[istart] + u[istart]*cos(ϕ[istart])) + (1/2)*(-1*vr[iend]*vt[iend]/r[iend] + u[iend]*cos(ϕ[iend])) + (1/12)*(vr[istart]^2*vt[istart]/r[istart]^2 - (vr[istart]*at[istart]+ar[istart]*vt[istart])/r[istart] - u[istart]*sin(ϕ[istart])*(ϕ[iend]-ϕ[istart])/dt + (u[iend]-u[istart])/dt*cos(ϕ[istart])) - (1/12)*(vr[iend]^2*vt[iend]/r[iend]^2 - (vr[iend]*at[iend]+ar[iend]*vt[iend])/r[iend] - u[iend]*sin(ϕ[iend])*(ϕ[iend]-ϕ[istart])/dt + (u[iend]-u[istart])/dt*cos(ϕ[iend])) ))
end (model, Min, dt*sum(u) + λ1*dt) set_optimizer(model, with_optimizer(Ipopt.Optimizer)); set_optimizer_attribute(model, "print_level", 3); optimize!(model) r_out = value.(r) θ_out = value.(θ) vr_out = value.(vr) vt_out = value.(vt) ar_out = value.(ar) at_out = value.(at) dt = value(dt) ϕ_out = value.(ϕ) u_out = value.(u) return Dict( "r" => r_out, "θ" => θ_out, "vr" => vr_out, "vt" => vt_out, "ϕ" => ϕ_out, "u" => u_out, "ar" => ar_out, "at" => at_out, "t" => convert(Array, 0:dt:N*dt) )endxxxxxxxxxx"""This is simply a utility function to run a simulation and plot its outputs."""function runHermiteTime(plotTitle, λ1=0.0, λ2=0.0, λ3 = 0.0 ;N, max_thrust, r_init, r_final) output = transferOrbitHermiteTime( λ1, λ2, λ3, N=N, max_thrust=max_thrust, r_init=r_init, r_final=r_final ) output = reconstructPaths(out_dis=output) print(size(output["t"])) fig = figure(figsize=(10,10)) # Create a new figure ax = PyPlot.axes(polar="true") # Create a polar axis PyPlot.title(plotTitle) p = scatter(output["θ"][end:-1:1], output["r"][end:-1:1], c=output["u"][end:-1:1], cmap="jet", s=1.0)
dtheta = 10 ax.set_thetagrids(collect(0:dtheta:360-dtheta)) # Show grid lines from 0 to 360 in increments of dtheta ax.set_theta_zero_location("N") # Set 0 degrees to the top of the plot ax.set_theta_direction(-1) # Switch to clockwise ax[:set_yticks](convert(Array, 0:0.5:r_final+0.5)) color_bar = PyPlot.colorbar() color_bar.set_label("Thrust") fig.canvas.draw() # Update the figure fig = figure("pyplot_subplot_mixed",figsize=(10,6)) subplot(321) plot(output["t"], output["r"]); title("Radius") subplot(322) plot(output["t"], output["u"]); title("Thrust") subplot(323) plot(output["t"], output["ϕ"]); title("Thrust Angle") subplot(324) plot(output["t"], output["vt"]); title("Tangential Velocity") subplot(325) plot(output["t"], output["vr"]); title("Radial Velocity") subplot(326) plot(output["t"], output["θ"]); title("Phase") fig.canvas.draw() # Update the figure suptitle("Transfer Orbit Profiles") fig.tight_layout()endxxxxxxxxxx# l = 1.1/4.0# l = 0.55 # Max nice# l = 0.00000001 # BADl = 0.001runHermiteTime( "Time Optimal Transfer Trajectory", l, 0.0, 0.0, N=60, max_thrust=0.01, r_init=2.0, r_final=6.0)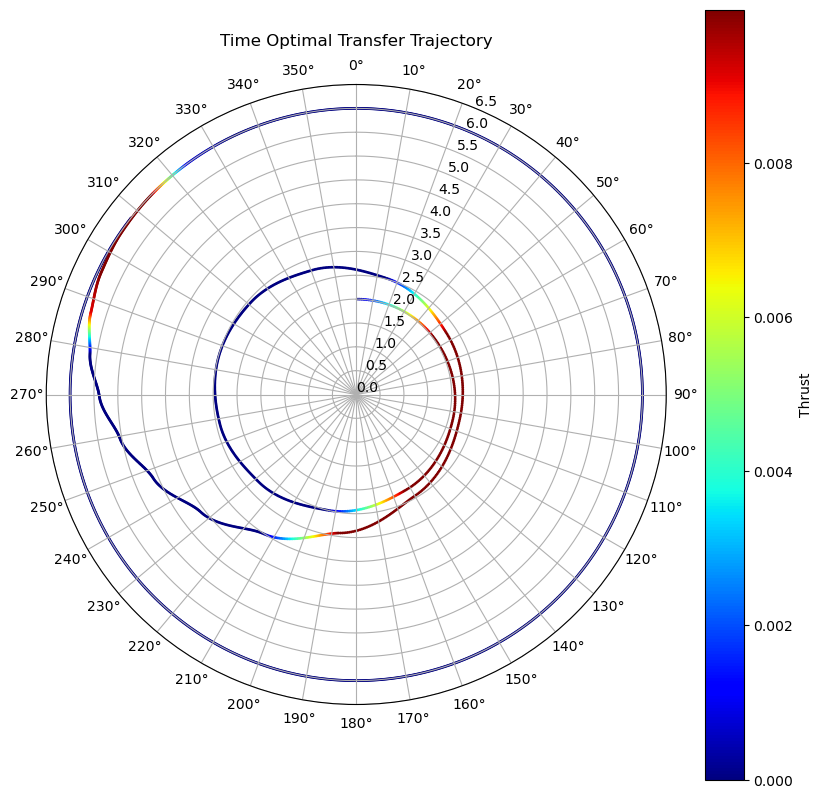

xxxxxxxxxxTotal number of variables............................: 481variables with only lower bounds: 121variables with lower and upper bounds: 0variables with only upper bounds: 0Total number of equality constraints.................: 363Total number of inequality constraints...............: 181inequality constraints with only lower bounds: 60inequality constraints with lower and upper bounds: 0inequality constraints with only upper bounds: 121Number of Iterations....: 237(scaled) (unscaled)Objective...............: 2.8805752505683396e-01 2.8805752505683396e-01Dual infeasibility......: 6.4126481902349042e-13 6.4126481902349042e-13Constraint violation....: 2.7478019859472624e-15 2.7478019859472624e-15Complementarity.........: 2.5059035597957591e-09 2.5059035597957591e-09Overall NLP error.......: 2.5059035597957591e-09 2.5059035597957591e-09Number of objective function evaluations = 291Number of objective gradient evaluations = 238Number of equality constraint evaluations = 291Number of inequality constraint evaluations = 291Number of equality constraint Jacobian evaluations = 238Number of inequality constraint Jacobian evaluations = 238Number of Lagrangian Hessian evaluations = 237Total CPU secs in IPOPT (w/o function evaluations) = 1.249Total CPU secs in NLP function evaluations = 1.721EXIT: Optimal Solution Found.(2950,)
We clearly are getting a much faster time to orbit, at the cost of higher fuel usage. However, this model of the problem seems to have many local minima. This cannot be the global optimum of the model, as the model keeps running once it has reached its final orbit. If it was at the global minimum, then it would stop once it reached the final orbit.
As such, we also investigated a penalty method for finding a pseudo time optimal orbit based on the fuel optimal model.
Pseudo Time Optimal
Below we use a penalty objective for the fuel optimal model that penalizes proportional to the distance the trajectory is at every time step from the final orbit radius.
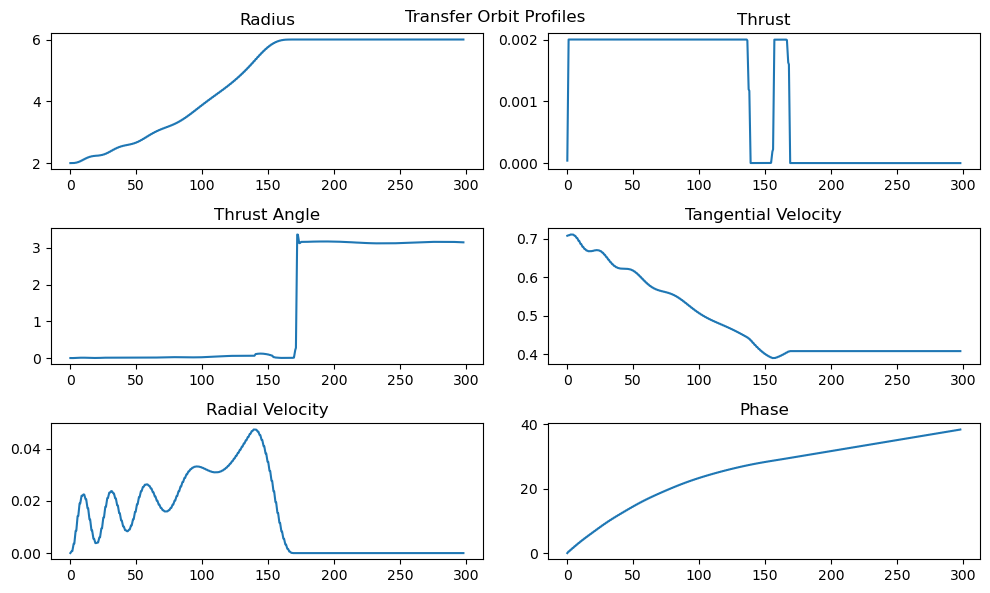
xxxxxxxxxxl = 0.0001runHermite( "Pseudo Time Optimum Transfer Trajectory", l, modelObjective=pseudoTime, T=300.0, N=200, max_thrust=0.002, r_init=2.0, r_final=6.0)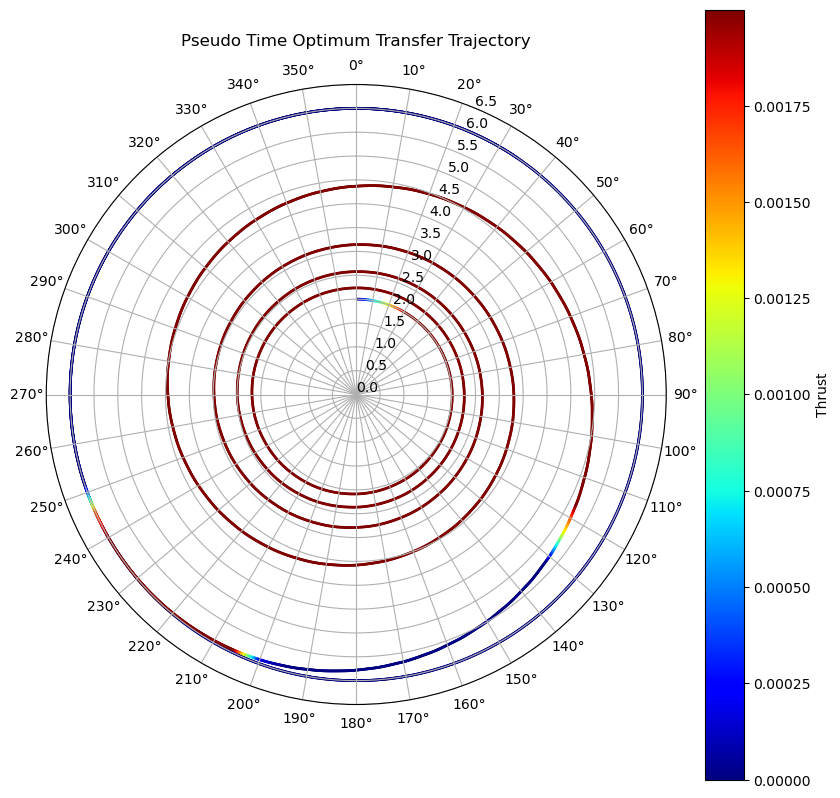
xxxxxxxxxxTotal number of variables............................: 1800variables with only lower bounds: 400variables with lower and upper bounds: 0variables with only upper bounds: 0Total number of equality constraints.................: 1203Total number of inequality constraints...............: 1000inequality constraints with only lower bounds: 600inequality constraints with lower and upper bounds: 0inequality constraints with only upper bounds: 400Number of Iterations....: 110(scaled) (unscaled)Objective...............: 2.2503528044705384e-01 2.2503528044705384e-01Dual infeasibility......: 5.0723425459864302e-11 5.0723425459864302e-11Constraint violation....: 6.5225602696727947e-15 6.5225602696727947e-15Complementarity.........: 2.5059035607398638e-09 2.5059035607398638e-09Overall NLP error.......: 2.5059035607398638e-09 2.5059035607398638e-09Number of objective function evaluations = 159Number of objective gradient evaluations = 111Number of equality constraint evaluations = 159Number of inequality constraint evaluations = 159Number of equality constraint Jacobian evaluations = 111Number of inequality constraint Jacobian evaluations = 111Number of Lagrangian Hessian evaluations = 110Total CPU secs in IPOPT (w/o function evaluations) = 1.552Total CPU secs in NLP function evaluations = 0.557EXIT: Optimal Solution Found.
We can clearly see that without the time penalty included in the objective, the model tries to get to orbit much faster by thrusting almost continuously the whole way. The details of this trajectory, and the study of different penalty multipliers hat follows, are discussed in the results section.
Pseudo Time Optimal
WARNING The next cell will take a bit to run. Usually takes about 3 minutes.
xxxxxxxxxx# l_set = [0.001, 0.00008, 0.00007, 0.0000675, 0.0000670, 0.0000665, 0.0000660, 0.0000655, 0.000065, 0.00006, 0.00005, 0.00004, 0.00003, 0.00002]l_set = convert(Array, 0.00002:0.00001/4:0.00008)
function pseudoTimeStudyCompute() all_outputs = Dict() for l in l_set output = transferOrbitHermite( l, modelObjective=pseudoTime, T=300.0, N=200, max_thrust=0.002, r_init=2.0, r_final=6.0 )
output = reconstructPaths(out_dis=output) all_outputs[l] = output end return all_outputsend
pseudo_time_output = pseudoTimeStudyCompute()xxxxxxxxxxTotal number of variables............................: 1800variables with only lower bounds: 400variables with lower and upper bounds: 0variables with only upper bounds: 0Total number of equality constraints.................: 1203Total number of inequality constraints...............: 1000inequality constraints with only lower bounds: 600inequality constraints with lower and upper bounds: 0inequality constraints with only upper bounds: 400Number of Iterations....: 204(scaled) (unscaled)Objective...............: 2.0349554301142975e-01 2.0349554301142975e-01Dual infeasibility......: 4.8865356205851640e-12 4.8865356205851640e-12Constraint violation....: 5.8564264548977008e-15 5.8564264548977008e-15Complementarity.........: 2.5059035596999075e-09 2.5059035596999075e-09Overall NLP error.......: 2.5059035596999075e-09 2.5059035596999075e-09Number of objective function evaluations = 263Number of objective gradient evaluations = 205Number of equality constraint evaluations = 263Number of inequality constraint evaluations = 263Number of equality constraint Jacobian evaluations = 205Number of inequality constraint Jacobian evaluations = 205Number of Lagrangian Hessian evaluations = 204Total CPU secs in IPOPT (w/o function evaluations) = 3.141Total CPU secs in NLP function evaluations = 0.938EXIT: Optimal Solution Found.
xxxxxxxxxx........................ Lots of similar output later .........................
xxxxxxxxxxioff()
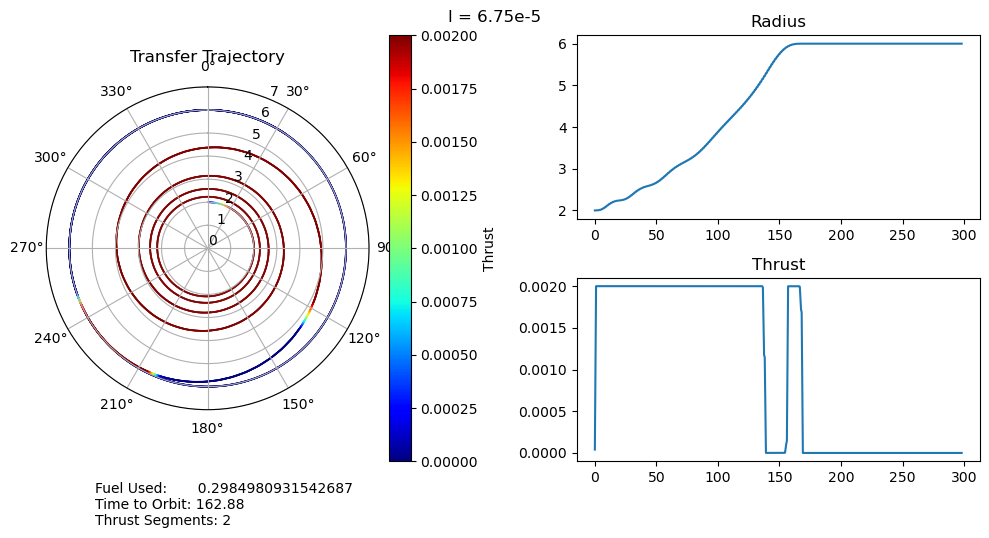
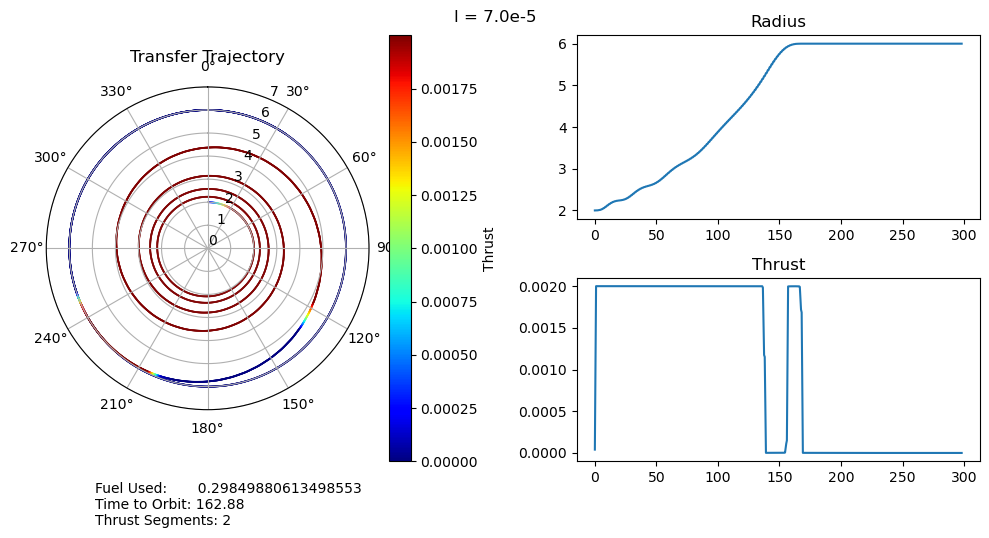
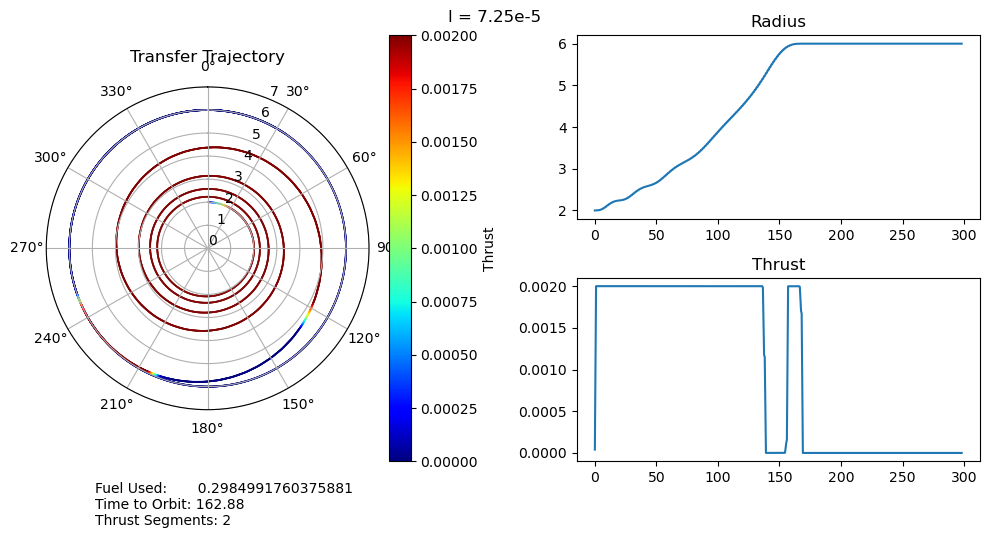
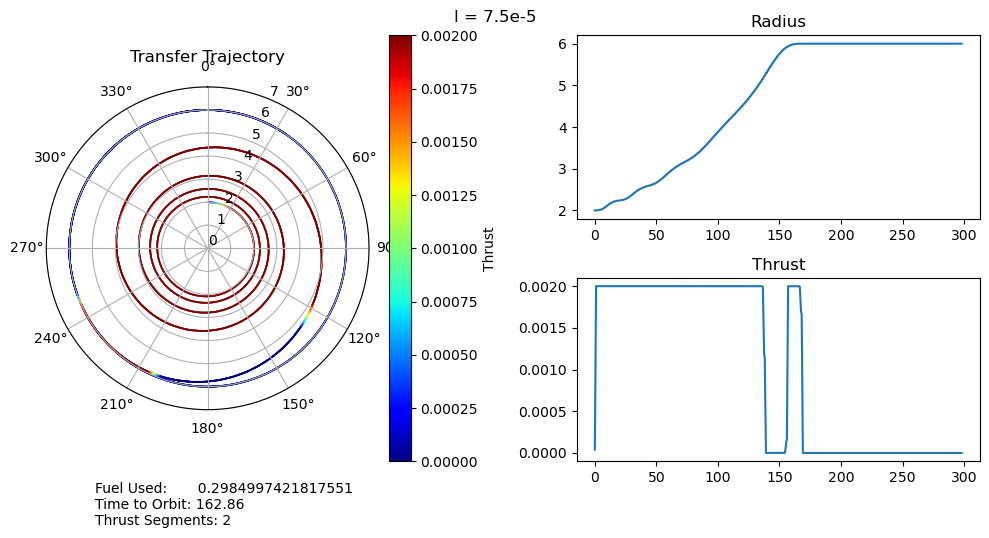
function smallOutput(;output, l, time_to_orbit, fuel_used, segments, count) fig = figure("pyplot_subplot_mixed$count",figsize=(10,5)) ax = subplot(121, polar="true") PyPlot.title("Transfer Trajectory") p = scatter(output["θ"][end:-1:1], output["r"][end:-1:1], c=output["u"][end:-1:1], cmap="jet", s=0.1)
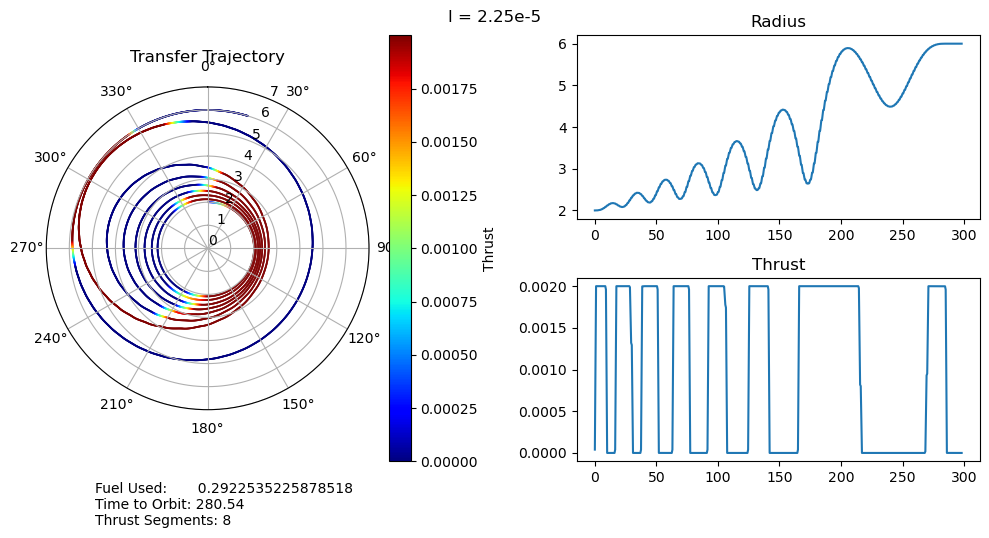
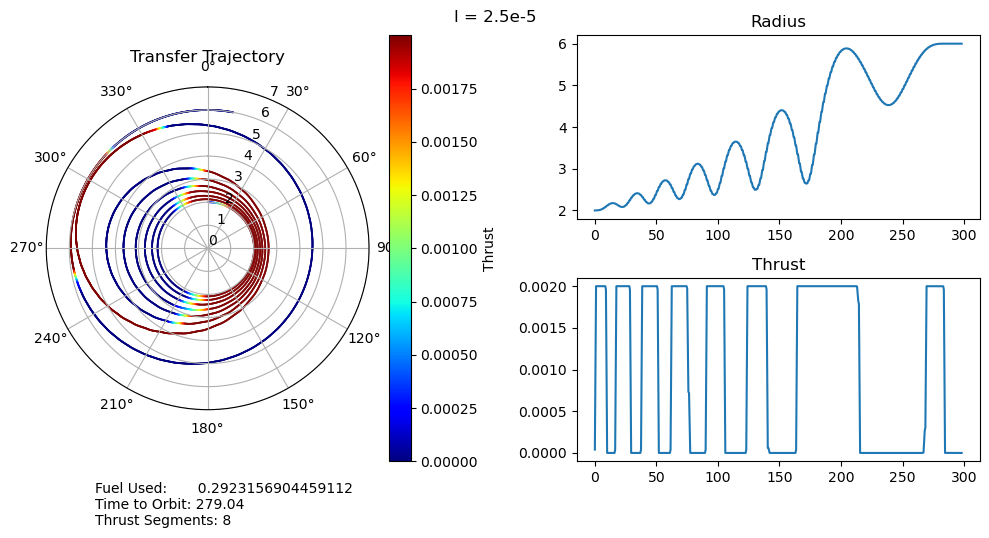
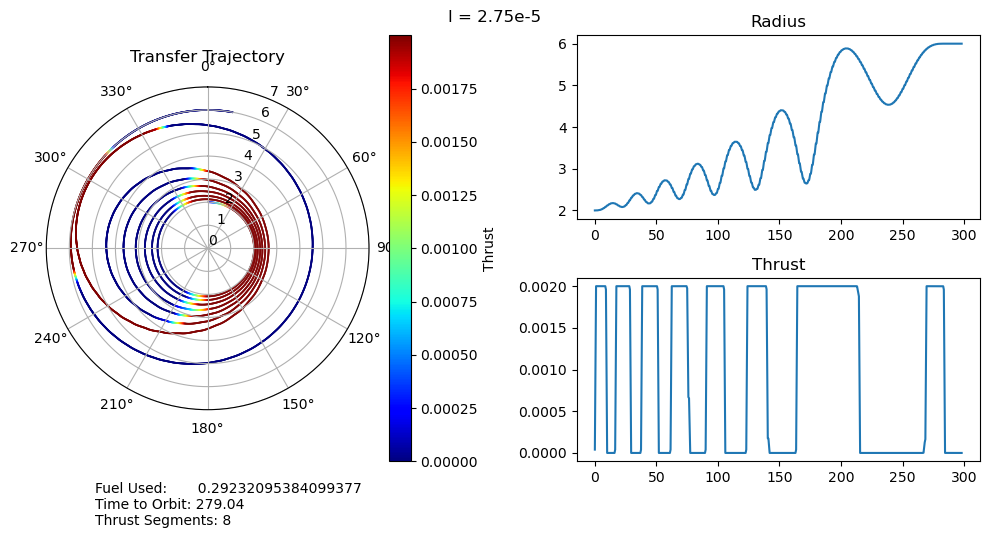
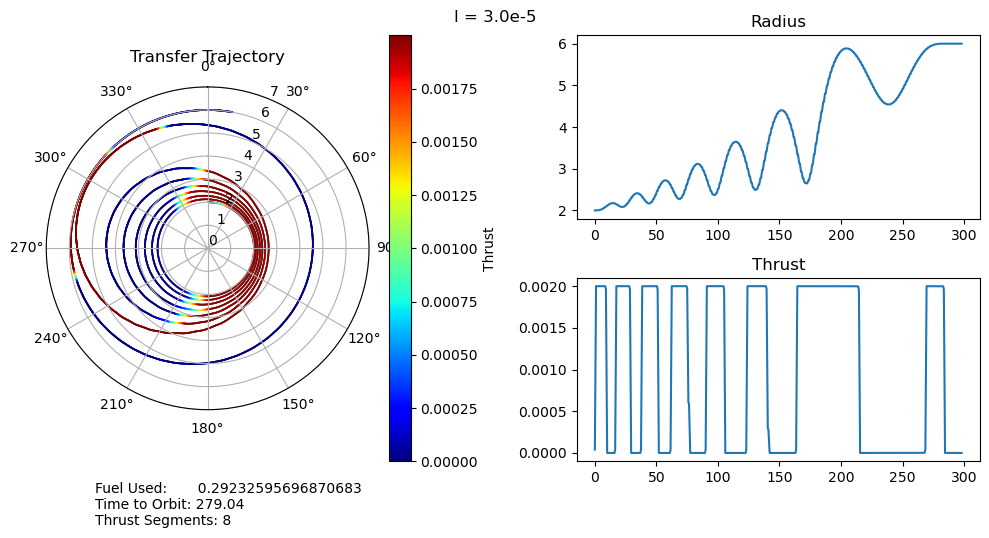
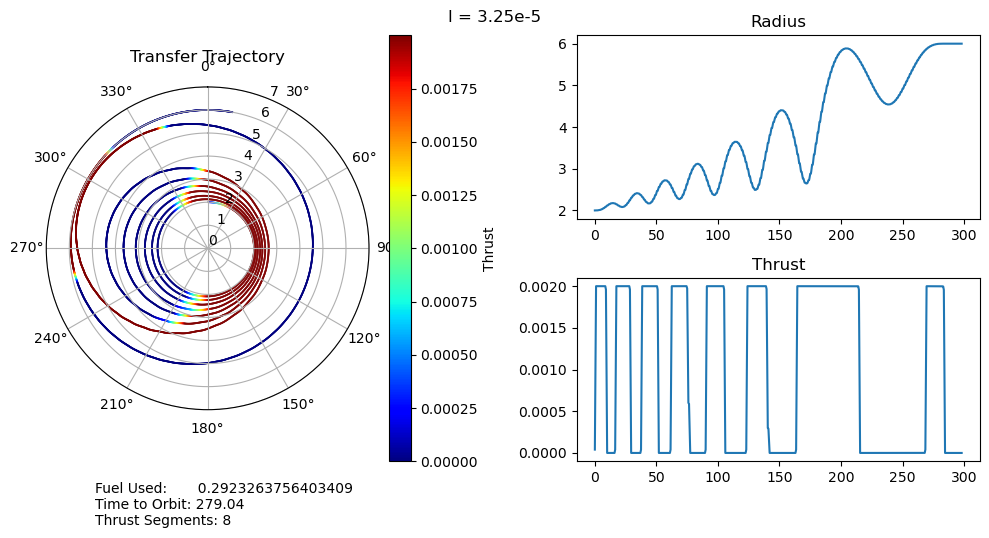
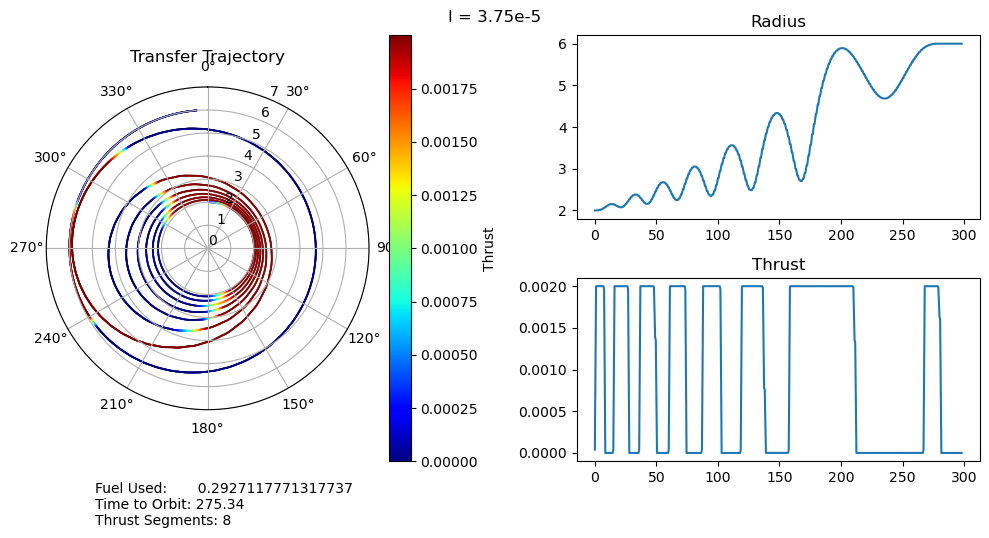
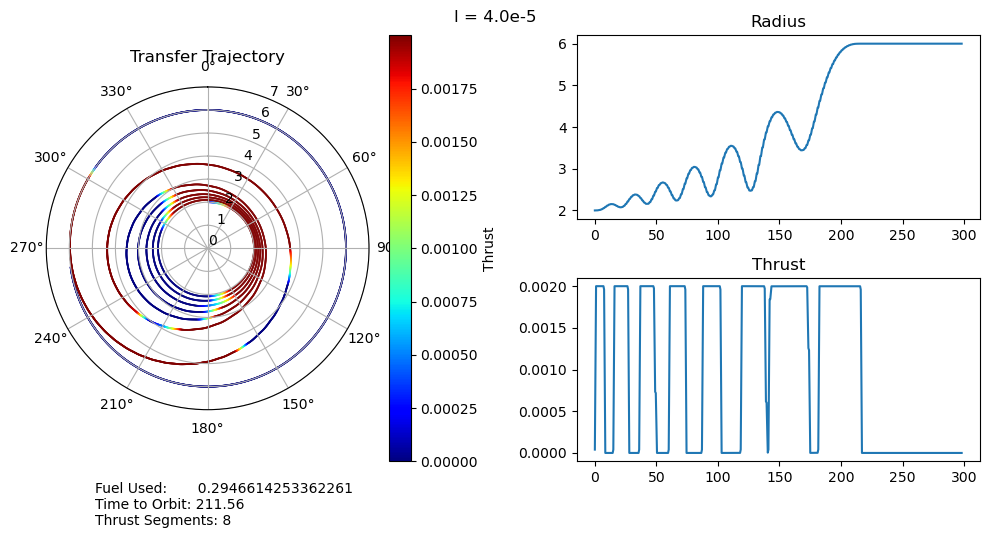
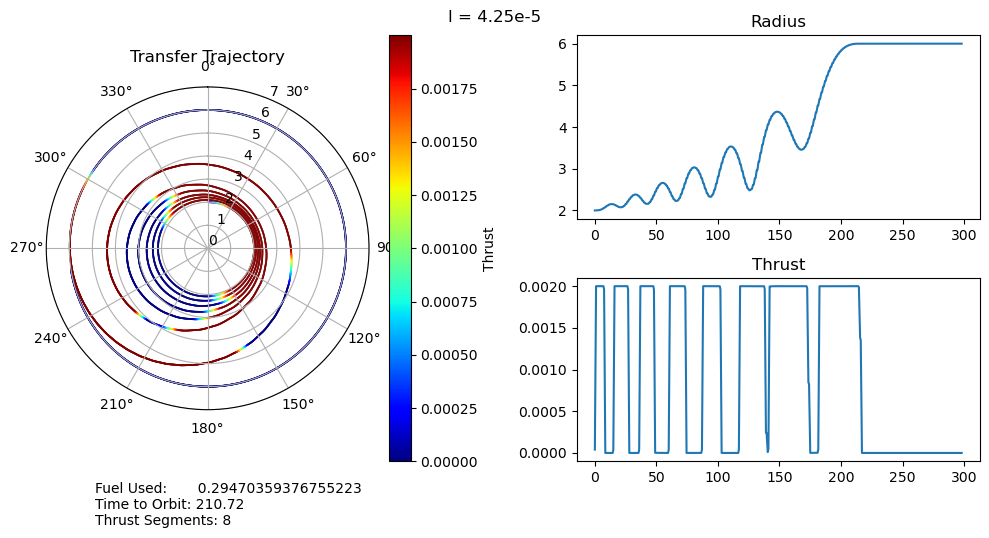
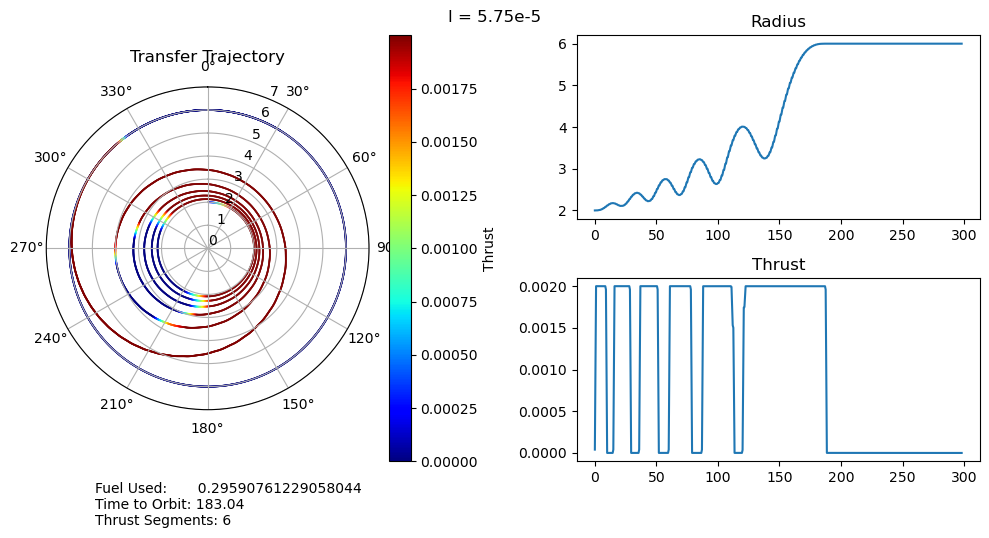
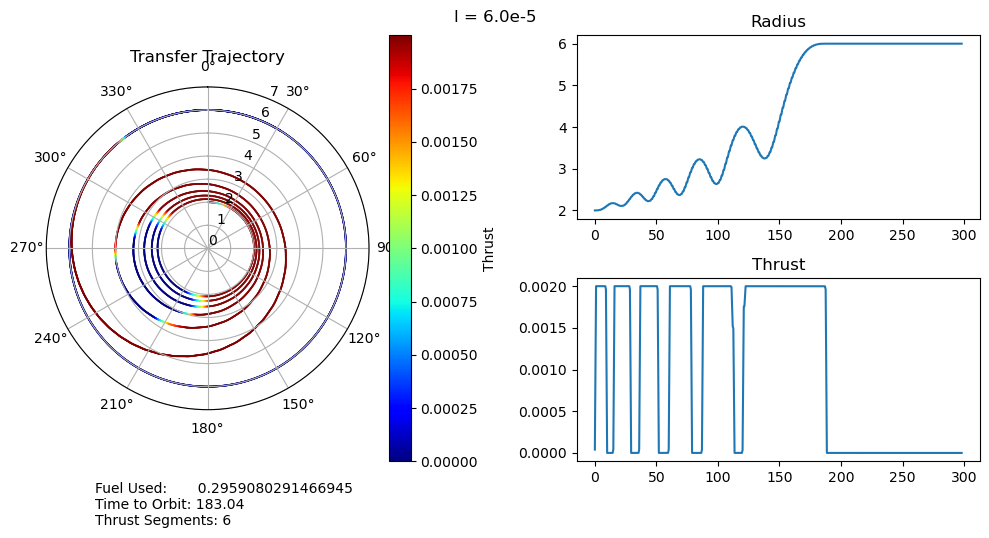
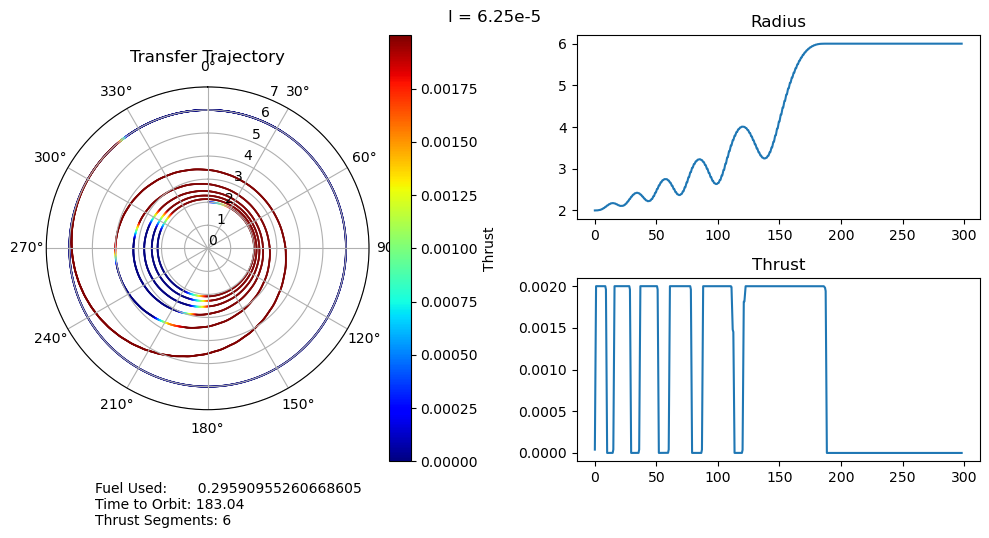
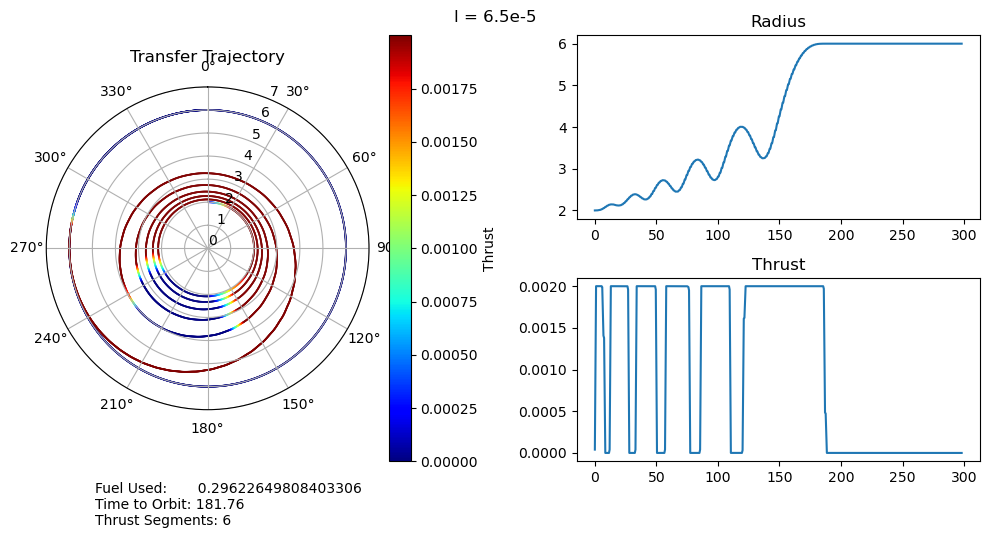
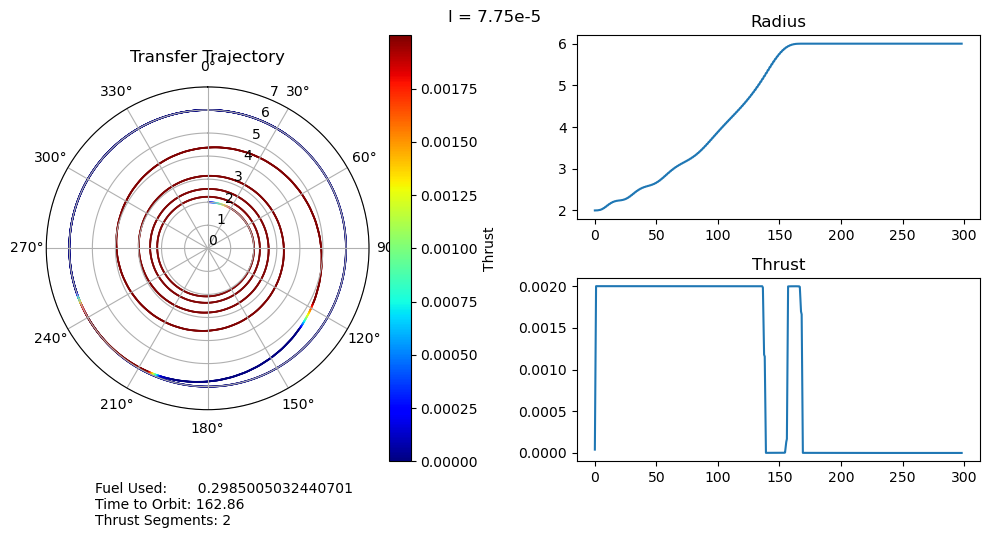
dtheta = 30 ax.set_thetagrids(collect(0:dtheta:360-dtheta)) # Show grid lines from 0 to 360 in increments of dtheta ax.set_theta_zero_location("N") # Set 0 degrees to the top of the plot ax.set_theta_direction(-1) # Switch to clockwise ax[:set_yticks](convert(Array, 0:1.0:7.0)) color_bar = PyPlot.colorbar() color_bar.set_label("Thrust") fig.canvas.draw() subplot(222) plot(output["t"], output["r"]); title("Radius") subplot(224) plot(output["t"], output["u"]); title("Thrust") suptitle("l = $l") fig.text(0.1, -0.05, "Fuel Used: $fuel_used\nTime to Orbit: $time_to_orbit\nThrust Segments: $segments" ) fig.canvas.draw() fig.tight_layout() # println("Fuel Used: ", fuel_used)# println("Time to Orbit: ", time_to_orbit)end
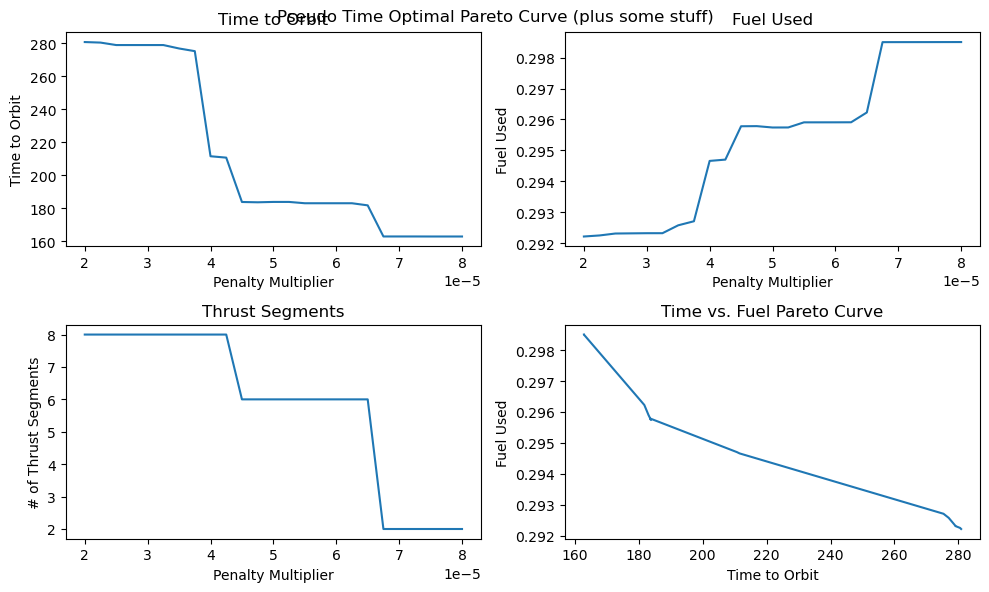
function pseudoTimeStudyAnalyze(;all_outputs, l_set) time_to_orbit = Dict() fuel_used = Dict() thrust_segments = Dict() for l in l_set time_to_orbit[l] = timeToOrbit(all_outputs[l], 6.0) fuel_used[l] = fuelUsed(all_outputs[l]) thrust_segments[l] = thrustSegments(all_outputs[l]) end count = 1 for l in l_set smallOutput( output = all_outputs[l], l = l, time_to_orbit = time_to_orbit[l], fuel_used = fuel_used[l], segments = thrust_segments[l], count = count ) count += 1 end fig = figure("pyplot_subplot_mixed$count",figsize=(10,6)) ax = subplot(221) plot(l_set, [time_to_orbit[l] for l in l_set]) xlabel("Penalty Multiplier") ylabel("Time to Orbit") title("Time to Orbit") ax = subplot(222) plot(l_set, [fuel_used[l] for l in l_set]) xlabel("Penalty Multiplier") ylabel("Fuel Used") title("Fuel Used") ax = subplot(223) plot(l_set, [thrust_segments[l] for l in l_set]) xlabel("Penalty Multiplier") ylabel("# of Thrust Segments") title("Thrust Segments") ax = subplot(224) plot([time_to_orbit[l] for l in l_set], [fuel_used[l] for l in l_set]) xlabel("Time to Orbit") ylabel("Fuel Used") title("Time vs. Fuel Pareto Curve") suptitle("Pseudo Time Optimal Pareto Curve (plus some stuff)") fig.canvas.draw() fig.tight_layout()endxxxxxxxxxxpseudoTimeStudyAnalyze(all_outputs = pseudo_time_output, l_set = l_set)

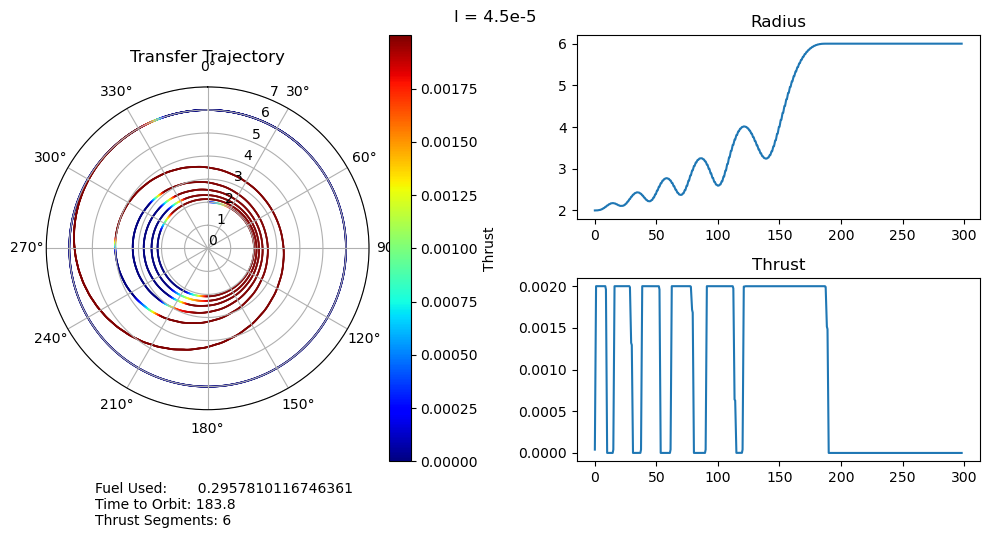
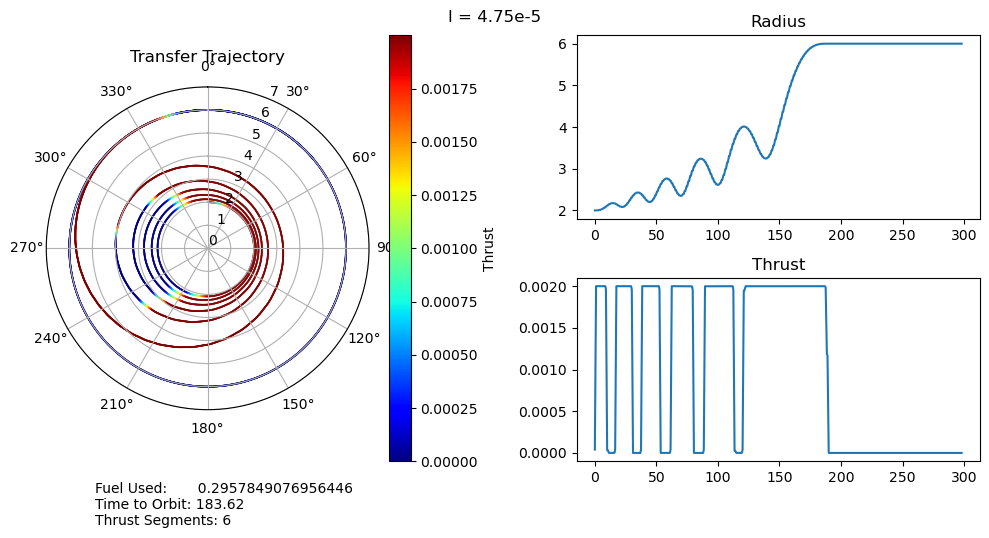

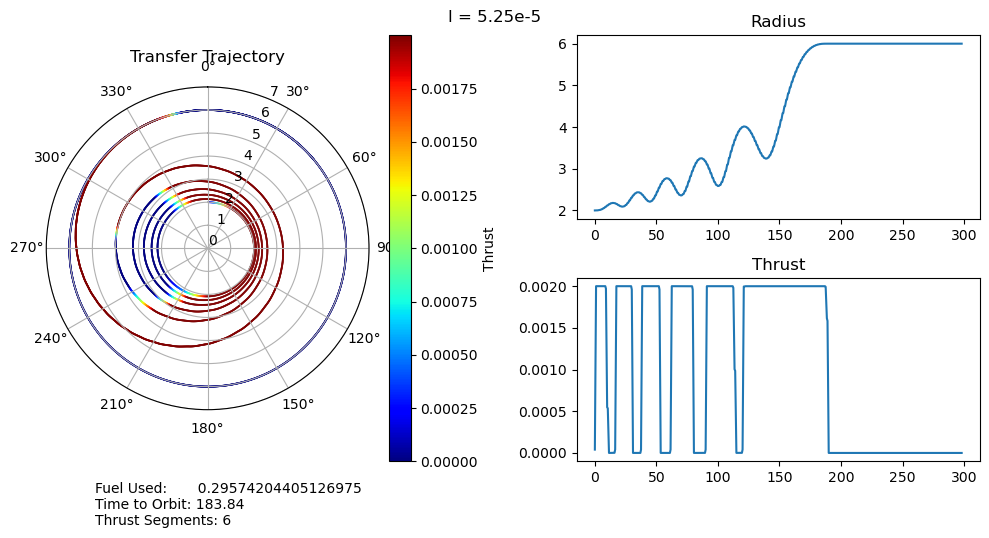
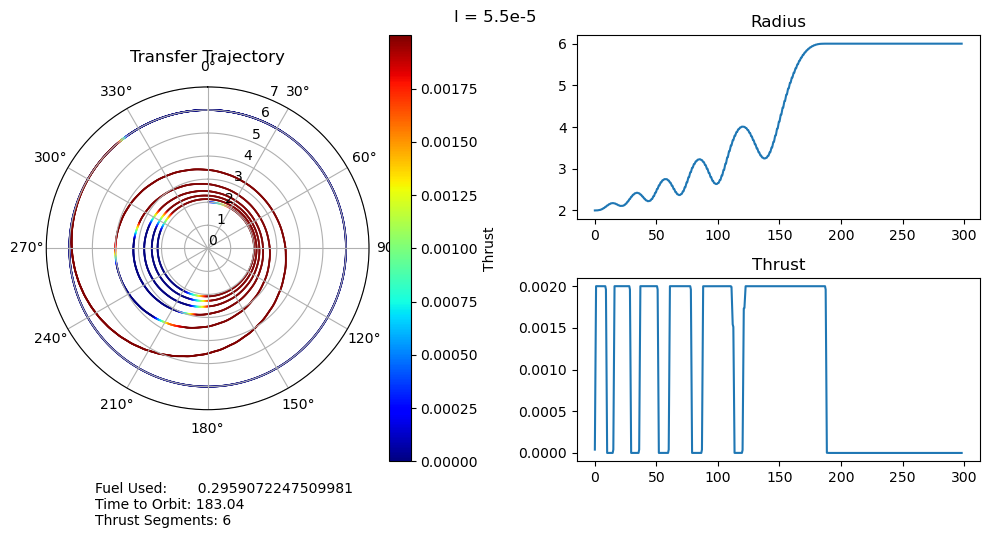
4. Results and Discussion
Fuel Optimal Problem
- Model assumes maximum time, maximum thrust, initial and final orbits
- Not super sensitive to starting conditions, but struggles when random
The solutions we found for the fuel optimal transfer trajectory very closely match what we expect based on our intuitive explanations of the physics (when and where can we most efficiently thrust in our orbit) and match the results obtained by others on this problem. Shown below is the fuel optimum transfer trajectory obtained by Topputo and Zhang in their paper "Survey of Direct Transcription for Low-Thrust Space Trajectory Optimization with Applications" in figure 15.
There are several parts of the model that we assumed:
- We have set an implicit maximum time for our transfer trajectory by only letting our time segments go out to
- The maximum thrust used is based on that seen in other papers. We did not base it off of a known engine or spacecraft's thrust.
- The mass of the spacecraft was assumed to be 1 in normalized units. The conversion to SI units was not done, so this may or may not be a realistic mass for a spacecraft.
Despite these assumptions, we expect our method, if not the exact trajectories, to optimize to physically and technologically realizable situations.
One important factor in the ability of our model to converge is the starting conditions. We set the starting conditions for each model to be a circular orbit at the initial altitude, so if the optimizer didn't change any variable, the problem would already satisfy all the dynamics constraints, and only violate the final condition constraints. Using these starting points we are able to consistently get the model to converge to at least local minima. Initially we did not set starting values, so they started at random values; this was consistently causing issues as the optimizer was rarely able to converge to realistic trajectories.
Time Optimal Problem
The truly time optimal model, where we made the time step
I suspect this is a combination of the extremely non-linear dynamics constraints and the form of the objective function such that it remains numerically stable. The truly physically relevant form of the objective function, one which does not depend on the number of time segments we choose to use to model the problem, seems to be particularly unstable. We were able to stabilize it a bit more by letting it implicitly depend on the number of time segments in the model, but even so, it was very inconsistent.
Because this approach presented so many problems, we also tried, and found great success with, the pseudo time optimal formulation of the problem.
Pseudo Time Optimal Problem
Compared to the time optimal model of the problem, we were able to retain the consistent stability of the fuel optimal problem while also letting us move between fuel and time optimal trajectories according to a single parameter of the problem.
I have several main observations about our results:
- The time optimal trajectories we found with large (8e-5) penalty multipliers closely match that of the Topputo and Zhang paper in figure 12. The main difference we observe is that their single thrust segment both raises and circularizes the orbits, whereas ours divides that into two separate stages. It is possible that their model simply has less dependence on fuel usage (it isn't clear exactly what objective function they used) than ours does, but even increasing our penalty multiplier, we also had two separate thrust segments.
- For small penalty multipliers we would expect, and do observe, that our trajectory matches that of the fuel optimal problem.
- A very unexpected feature of our results is the discontinuous jumps between the number of thrust segments as we move along the Pareto curve. It abruptly drops from 8 to 6, bypassing 7, and then again drops from 6 to 2, bypassing 3, 4, and 5. I cannot explain this at the moment, as I would expect it to progressively decrease the number of orbits, and therefore the number of thrust segments, it does. One possible explanation is that this is simply an artifact of our optimization, and that these are local minima rather than global minima. This is definitely possible, but all of the problems started from the same position, so I would expect every one to move through approximately the same space as they converge to their solutions. It wouldn't make much sense for multiple orbits to be consistently skipped if it was just an artifact of the optimizer.
- We can also observe that both the time to orbit and the fuel usages plateau at both extremes of the penalty multiplier range we investigated. We tested manually and observed that the performance increases beyond this range were fairly minimal.
5. Conclusion
Our findings are discussed in the previous section. There are a large number of possible directions we could take this in the future, including:
- 3D orbits. By expanding our model to include orbit inclination, RAAN, and argument of perigee, we could investigate more realistic trajectories for satellite maneuvers around Earth. One especially interesting problem to investigate in 3D is the optimal trajectories for plane change maneuvers, as that is closely tied to your proximity to the ascending and descending nodes of your orbit.
- Two body system. This would be especially interesting to look at. We could look at trying to recreate lunar injection trajectories. This can also be expanded to 3D, though I'm not sure if that would significantly change the trajectories.
- Multi body system. This would let us look at trajectories in the ecliptic of the solar system. If we were able to model the dynamics due to both the sun and nearby bodies, we may be able to find tours of the solar system similar to what the Voyager probes used in the 70s to fly by many of the planets, and eventually escape the solar system.
- Non circular orbits. In this project we only looked at circular orbits, but many satellites operate in highly elliptic orbits about Earth. Specifically, the Soviets launched GLONASS satellites into highly elliptical polar orbits such that they will always have coverage over the arctic and northern Russia. The traditional GPS and GLONASS constellations can't reach that far North. Investigating trajectories to get into these orbits may be interesting.
- Orbit rendezvous are extremely important now and will be in the future as we expand our capabilities in space. In this project I only cared about the final shape of the trajectory, not being in a given phase at a given time as we would need if we were meeting a body already in orbit. This could be achieved by hacking our current model a bit without adding any additional constraints. If we assume that the craft we are meeting is in a known stable orbit, then we can calculate ahead of time where it will be, and constrain our ending point to be in sync with it.
- Coverage optimality. Many satellites currently perform imaging or science looking at different parts of the sky or of Earth. We may want to be able to cover as much of the sky or Earth as possible from our orbit(s), and so finding trajectories and stable orbits that meet these criteria could be very interesting.
In the case of the multiple body systems, I believe we would have to resort to Cartesian coordinates, which would make our dynamics much uglier than they are now. I don't believe we would be able to super impose multiple polar coordinate systems and get the physics to work out for us.
The 3D orbit problem would just be the addition of a couple more dynamics constraints and state variables, and should be readily doable.